This logic puzzle is unlike others in that it also shows you how your brain works when it thinks logically.
In a video posted to the YouTube channel for WonderWhy, the narrator explains how a 'logic test' from 1963 by Peter Wason can help you to understand how logical your brain is. Only four per cent of participants in the 1963 test got it right and 46 per cent of people get it wrong in exactly the same way! Take a look to see how you fare.
Wason's four card selection test was conducted in 1970 for the first time and ever since it has been a good judge of a person's logical reasoning.
The test uses four cards. Each card has one letter on one side and one number on the other.
Picture: WonderWhy/YouTube
Participants are shown four cards and told the rule: If a card has a vowel on one side, it must have an even number on the other side.
Picture: WonderWhy/YouTube
The test is this: Which card(s) must be turned over to determine whether or not the rule has been followed?
Looking at these cards, can you work it out? Scroll down for the answer (and find out why so many people get it wrong):
Sign up to our new free Indy100 weekly newsletter
If you said 'A' and '7' you were right. Well done you.
If you said 'A' and '2' you were wrong, but so were 46 per cent of other participants. Any other answers, what's wrong with you?
Here's why:
The task was to determine if the rule has been 'followed' by turning over the cards, and the best way to do this is to attempt to disapprove the rule.
Card A if turned over should show an even number (in which case the rule is correct) and if it showed an odd number it would disprove the rule.
Card K if turned over could show an odd number or an even number. It's basically an irrelevant card.
Card 2 is where most people make their mistake.
That's because of a misreading of the rule: 'If a card has a vowel on one side, it must have an even number on the other side.' People who try and use Card 2 are trying to make the rule work both ways. It doesn't. This is a 'if' and 'then' statement. So if Card 2 is turned over and it shows a consonant, the rule has not been broken. As such there is no need to turn it over.
Card 7 if turned over should not show a vowel. If it shows a vowel, then the rule has been broken and therefore the card is worth turning over.
Picture: WonderWhy/YouTube
So why do so few people get this logical puzzle right?
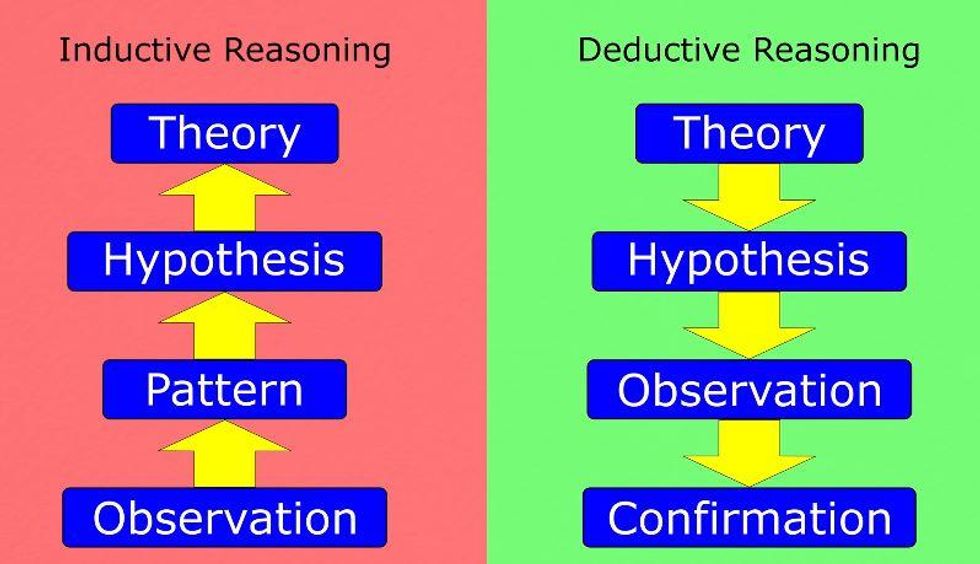
It's all to do with 'Inductive' and 'Deductive' reasoning, the latter of which was championed during the Enlightenment.
The inductive reasoning understands the statement:
If a card has a vowel on one side, it must have an even number on the other side.
In deductive reasoning, a person incorrectly believes that this statement is the same thing as:
If a card has an even number on one side, it must have a vowel on the other side.
This mistake is also known as 'Confirmation bias'.
Picture: WonderWhy/YouTube
Another reason is because logic is something we apply to real life. People do better at this puzzle when the letters and numbers are substituted for real world examples.
Watch the video from WonderWhy for more about this simple yet difficult logic puzzle:
Video: WonderWhy/YouTubeThe 'psychology of reasoning' as this field is sometimes known is as fascinating as that puzzle feels infuriating.
Have your say in our news democracy. Click the upvote icon at the top of the page to help raise this article through the indy100 rankings.