How high can you count on your fingers? The answer is much more than you'd think

How high can you count using just your fingers?

Seriously, give it a go – no matter how high you’ve managed, we can help you get higher.

Research mathematician James Tanton created a TED-Ed video explain how you can make your digits reach even more digits.

Most people will say that you can count to ten, with eight fingers and two thumbs.

Slightly more advanced people will know you can go up to twelve on one hand, if you divide your four fingers into three sections, with your thumb as the counter – double that for two hands means you can go up to 24.

Similarly, if you keep to one hand, and use the other to count each time you get to 12, you can have five groups of twelve – or 60.

Using the sections on the second hand will bring you up to 144.

There's more...

Here’s where it gets interesting. You can count higher by finding more countable sections on your hand.

There are three sections per finger and three creases – giving you six things to count. With this in mind, you now have 24 on each hand, bringing the total to 48. If you use one hand to mark groups of 24, you can get up to 576.

Ok, so six might be the limit of finger parts you can count, but that doesn’t mean it’s over.

Enter positional notation – this is when the placement of symbols allows for different values. The example Tanton gives is 999 – each nine represents a different value.

With this in mind, let’s assume there are two hand movements – up and down. By using a binary – that is, each number is double the previous number – and assigning each finger a different value, you can go a lot higher.

Let's say you want to present the number 250. You do 128+64+32+16+8+2=250

You can represent the three digit number with just six fingers raised.

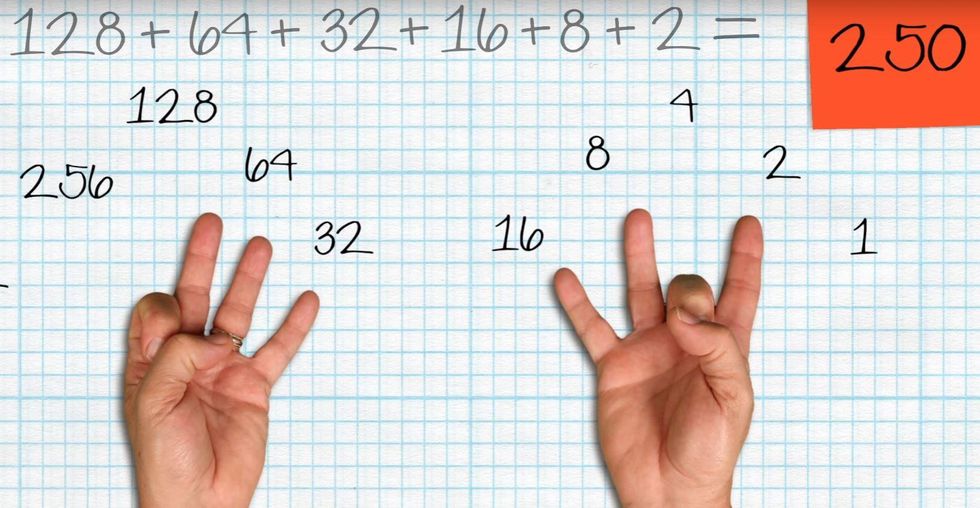
With this theory, you are able to get up to 1023.

Finally, if you can bend your finger half way, you have three states – down, half bent and raised, and you can use a base three positional system.

This gives you a grand total of 59,048

PHEW.

There you go, rediscovering your fingers, one article at a time.

Computers work much the same way, Tanton concludes in the video, below:

Pictures: TED-Ed/YouTube/screengrab

More: 18 uncool things that have become cool again

More: Can you work out this old school maths puzzle dividing the internet?